Odwrotna notacja polska
Odwrotna notacja polska została opracowana przez australijskiego naukowca Charlesa Hamblina jako "odwrócenie" beznawiasowej notacji polskiej Jana Łukasiewicza na potrzeby zastosowań informatycznych. Hamblin sugerował, aby notację tę nazwać "Azciweisakul notation" (Notacja Azciweisakuł - "Łukasiewicza" pisane od tyłu).
Notacja Łukaszewicza zakładała, że w przypadku wyrażeń najpierw podaje się operator, a później operandy. Początkowo służyła do zapisu wyrażeń logicznych, jednak później także arytmetycznych.
Przykładowy zapis wyrażenia: 8 / ( 3 + 1 )
w notacji polskiej będzie wyglądał następująco: / 8 + 3 1
co można odczytać jako "podziel 8 przez sumę 3 i 1"
W przypadku zapisu w odwrotnej notacji polskiej, najpierw występują operandy, a następnie operator. Powyższe wyrażenie zapisane w ONP będzie miało postać: 3 1 + 8 /
Jak widzimy jest to odwrotny zapis, niż w notacji Łukaszewicza. ONP używana jest obecnie w niektórych językach programowania, komputerach, a także niektórych kalkulatorach naukowych np. firmy Hewlett-Packard.
Praktyczność tego rozwiązania polega na łatwości implementacji oraz rezygnacji z nawiasów. Koniecznością jest wykorzystanie struktury danych, zwanej stosem. Obliczenie wartości wyrażenia zapisanego w ONP ilustruje poniższy algorytm:
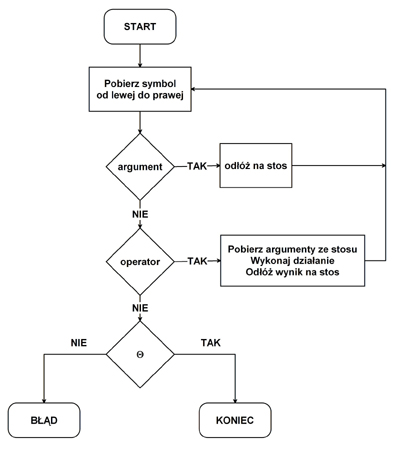
Poniższy przykład ilustruje działanie algorytmu. W tabeli przedstawiono stan wejścia, wartości, które aktualnie znajdują się na stosie oraz stan wyjścia.
Obliczanie wartości wyrażenia zapisanego w ONP: 6 4 * 1 + 4 *
| 6 | ||
| 6 4 | ||
| 24 | ||
| 24 1 | ||
| 25 | ||
| 25 4 | ||
| 100 | ||
| 100 |
Interaktywne ćwiczenie dotyczące obliczania wyrażeń w ONP
Aby móc dokonać obliczeń w odwrotnej notacji polskiej, konieczna jest konwersja wyrażenia zapisanego w arytmetyce nawiasowej do odpowiedniej formy. Można tego dokonać za pomocą algorytmu przedstawionego na poniższym rysunku:
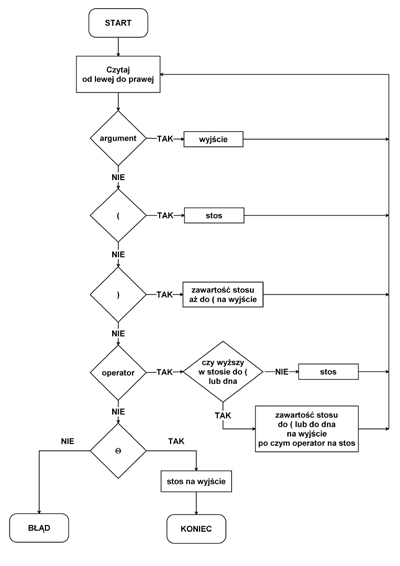
Poniższy przykład ilustruje działanie algorytmu. W tabeli przedstawiono stan wejścia, wartości, które aktualnie znajdują się na stosie oraz stan wyjścia.
Przekształcenie na odwrotną notację polską wyrażenia zapisanego w arytmetyce nawiasowej: ( 3 * 4 + 3 ) / 5
| ( | ||
| ( | 3 | |
| ( * | ||
| ( * | 4 | |
| ( + | * | |
| ( + | 3 | |
| + | ||
| / | ||
| / | 5 | |
| / |
Otrzymujemy wyrażenia zapisane w ONP: 3 4 * 3 + 5 /
Interaktywne ćwiczenie dotyczące konwersji wyrażenia zapisanego w notacji infiksowej na ONP