Lingwistyka matematyczna

Poniższy przykład zilustruje budowę diagramu składni dla gramatyki, mającej postać:

S : : = W ; Z
Z : : = W ; Z |
W : : = P | P O W
P : : = L | ( W )
L : : = C | C L
C : : = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
O : : = * | : | + | - | ^

Z powyższej gramatyki możemy wyprowadzić dowolne ciągi liczb całkowitych, oraz operacji arytmetycznych (mnożenie, dzielenie, dodawanie, odejmowanie, potęgowanie). Aby jednak można było skonstruować diagram składni dla danej gramatyki, należy sprawdzić, czy spełnia ona założenia gramatyk klasy LL(1). W tym przypadku, w definicje symboli W i L nie spełniają pierwszej reguły gramatycznej, dlatego też należy przeprowadzić lewostronną faktoryzację.
Poprawiona gramatyka będzie miała postać:

S : : = W ; Z
Z : : = W ; Z | ε
W : : = P W'
W' : : = O W | ε
P : : = L | ( W )
L : : = C L'
L' : : = L | ε
C : : = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
O : : = * | : | + | - | ^

Kolejne symbole możemy tak poprawionej gramatyki możemy przedstawić za pomocą następujących diagramów składni:

S
Z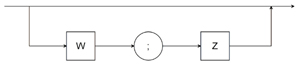
Z (po redukcji)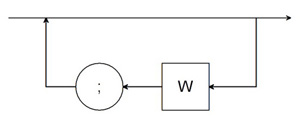
W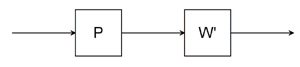
W'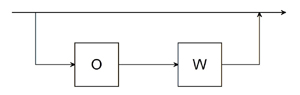
W (po redukcji)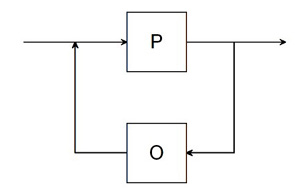
P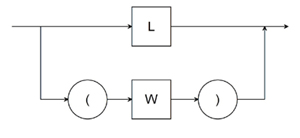
L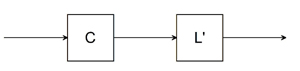
L'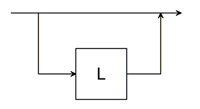
C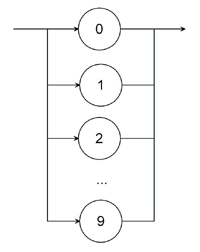
O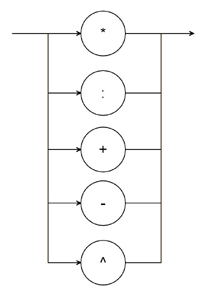

Aby skonstruować deterministyczne diagramy składni należy podstawić kolejne diagramy, które można zredukować, upraszczając ostateczny diagram. Powyższe diagramy można uprościć do następujących postaci:

S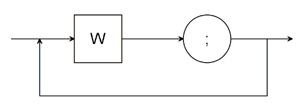
W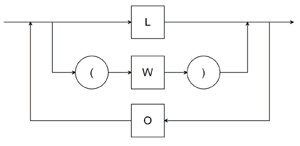
L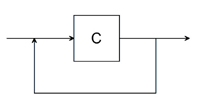

Diagramy odpowiadające symbolom C i O pozostają bez zmian. Po podstawieniu diagramów dla symboli L, O i C do diagramu dla symbolu W otrzymujemy:

W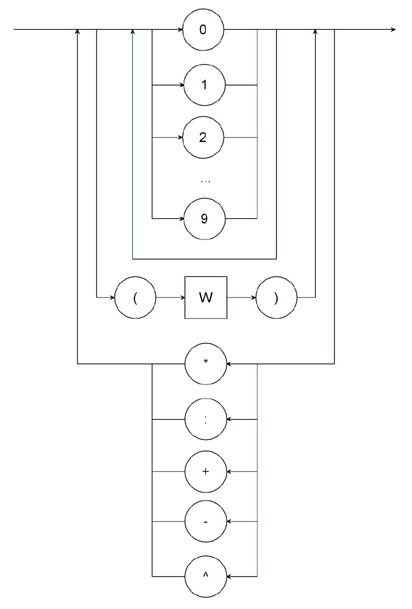

Diagram dla symboli S i W stanowią zbiór deterministycznych diagramów składni dla gramatyki