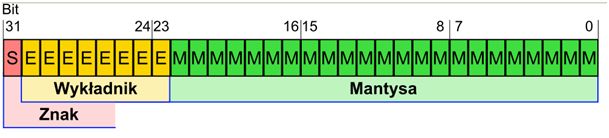
Standard IEEE 754

Standard IEEE 754 został opracowany po to aby ujednolicić wyniki obliczeń numerycznych wykonywanych na różnych platformach sprzętowych. Definiuje on dwa rodzaje liczb zmiennoprzecinkowych, 32 bitowe oraz 64 bitowe. Liczby 32 bitowe są określane jako "pojedynczej precyzji", natomiast liczby 64 bitowe są określane jako "podwójnej precyzji". Kod binarny liczby zmiennoprzecinkowej podzielony jest na 3 pola zawierające poszczególne komponenty zapisu zmiennoprzecinkowego.

Rys.Poszczególne komponenty zapisu zmiennoprzecinkowego

Pierwszy bit w zapisie jest bitem znaku, jeśli jest on zerem to liczba jest dodatnia jeśli jedynką to liczba jest ujemna. Jeżeli chcemy dokonać zmiany znaku liczby zmiennoprzecinkowej na przeciwny wystarczy zanegować ten bit.
Kolejne bity to bity cechy odpowiedzialne za kodowanie wykładnika potęgi 2, w pojedynczej precyzji jest ich 8. Liczby zmiennoprzecinkowe zakodowane w standardzie IEEE 754 zapisują cechę w kodzie z nadmiarem. Dla pojedynczej precyzji nadmiar wynosi 127. Zatem w polu cechy można zapisać wartość od -127 do 127. W podwójnej precyzji cecha zbudowana jest z 11 bitów co daje nadmiar 1023 oraz możliwość zapisania wartości od -1023 do 1023.
Ostatnim komponentem zapisu są bity ułamkowe mantysy. W pojedynczej precyzji mantysa posiada 23 bity, a w podwójnej 52. Wzrost liczby bitów mantys liczb zmiennoprzecinkowych wpływa na dokładność odwzorowania liczb rzeczywistych.

Wartość liczby zapisanej w standardzie IEEE 754.
Wartość liczby zapisanej w standardzie IEEE 754 obliczamy za pomocą wzoru:

L₍₁₀₎ = (-1)^z2^(c-127)(1.m)

Żeby móc zastosować powyższy wzór należy najpierw wydzielić z kodu poszczególne omawiane wcześniej komponenty. Są to bit znaku, bity mantysy oraz bity kodu cechy.

Przykład:

Chcemy poznać wartość dziesiętną liczby:
01000010110010000000000000000000_{(IEEE 754)}.

Dzielimy liczbę na poszczególne grupy:

z = 0 - liczba jest dodatnia
c = 10000101(NADMIAR=127) = 133 - 127 = 6
m = 01,10010000000000000000000_(U1) = 1¹⁹/₁₆
Mamy wszystkie niezbędne składniki, wyliczamy wartość liczby:

L₍₁₀₎ = (-1)^z2^(c-127)(1.m) = (-1)⁰ x 2⁶ x 1⁹/₁₆ = 2⁶ x ²⁵/₁₆ = 4 x 25 = 100

Zakres liczby zapisanej w standardzie IEEE 754.
Zakres liczby zapisanej w standardzie IEEE dla pojedynczej precyzji wynosi:

Z_{(IEEE 754)} = -3,4 x 10³⁸ ... 3,4 x 10³⁸

Natomiast dla podwójnej precyzji:

Z_{(IEEE 754)} = - 1,8 x 10³⁰⁸ ... 1,8 x 10³⁰⁸