Automaty skończone
Automat skończony jest abstrakcyjnym modelem matematycznym zachowania systemu dynamicznego o dyskretnych wejściach i wyjściach. System taki może znajdować się w jednym ze skończonej liczby stanów. Stan systemu stanowi podsumowanie informacji dotyczącej poprzednich wejść, która jest potrzebna do określenia zachowania systemu przy następnych wejściach.
Automat skończony składa się ze skończonego zbioru stanów i zbioru przejść ze stanu do stanu, zachodzących przy różnych symbolach wejściowych, wybranych z pewnego alfabetu . Dla każdego symbolu wejściowego istnieje dokładnie jedno przejście z każdego stanu odpowiadające temu symbolowi. Jeden ze stanów, oznaczany zazwyczaj symbolem q0, jest stanem początkowym, od którego automat rozpoczyna działanie. Niektóre ze stanów pełnią rolę stanów końcowych.
Automat skończony definiowany jest jako uporządkowana piątka:
M = ( Q, Σ, δ, q0, F )
gdzie:
Q - skończony zbiór stanów
Σ - skończony alfabet wejściowy
δ - funkcja przejścia odwzorowująca Q × Σ w Q
q0 - stan początkowy należący do Q
F - zbiór stanów końcowych
Wynika stąd, że δ przyporządkowuje każdemu stanowi q i każdemu symbolowi wejściowemu a nowy stan δ ( q, a )
Automat skończony możemy przedstawić jako układ o skończonej liczbie stanów, który znajduje się w pewnym stanie należącym do Q i czyta ciąg symboli z Σ, zapisany na taśmie w sposób pokazany poniżej:

Podczas jednego ruchu automat skończony, który aktualnie znajduje się w stanie q i czyta symbol a, przechodzi do stanu δ ( q, a ) i przesuwa głowicę o jeden symbol w prawo. Jeżeli δ ( q, a ) jest stanem akceptującym, uważamy że automat przyjął ciąg znaków z taśmy wejściowej, aż do pozycji na którą aktualnie przesunęła się głowica.
Poniżej przedstawiono przykład diagramu przejść automatu skończonego:
M = ( Q, Σ, δ, q0, F ) Q = { q0, q1, q2, q3 ) Σ = { 0, 1 } F = q0 |
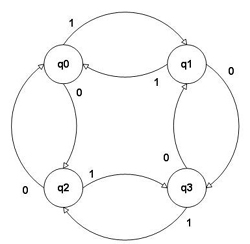 |
Oraz tabelę z funkcją przejścia dla tego automatu skończonego:
Przykładowymi słowami należącymi do L(M) są: 11, 10, 1010, 0101, 110110 etc.