Maszyna Turinga
PRZYKŁADY
Poniżej przedstawiono kilka przykładów maszyn Turinga. Pierwszy i najprostszy z nich odnosi się algorytmu negacji wartości binarnej.
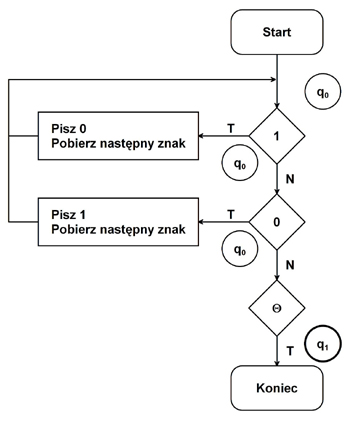
Kolumny poniższej tabeli są to elementy zbioru Q, czyli dopuszczalne stany maszyny Turinga, zaś wiersze oznaczają wszystkie dopuszczane symbole wejściowe, czyli te, które odczytuje głowica po wykonaniu ruchu.
| q1, -, - | |||
| q1, -, - |
W poszczególnych komórkach tabeli zapisano instrukcje dla maszyny. Przykładowy zapis q0, 1, P oznacza, że następnym stanem, w który wejdzie maszyna po przejściu z aktualnego będzie stan q0. Druga wartość oznacza, że głowica maszyny, będącej w aktualnym stanie ma zapisać na taśmie 1. Trzecia wartość informuje o tym, w którą stronę ma się przesunąć głowica (L - w lewo, P - w prawo).
Kolejnym przykładem ilustrującym działanie maszyny Turinga może być algorytm rozpoznawania w zbiorze napisów trójliterowych słowa "abc". Algorytm ilustrujący przytaczany przykład przedstawiono poniżej:

Podobnie jak w poprzednim przypadku, kolumny tabeli zawierają dopuszczalne stany maszyny, wiersze wszystkie dopuszczalne symbole wejściowe, a w komórkach zapisano instrukcje. q4 jest stanem odrzucającym, zaś q5 stanem akceptującym. P oznacza przesunięcie głowicy w prawo.
| q4, -, - | |||
| q3, -, P | |||
| q4, -, - | |||
| q4, -, - | |||
| q5, -, - |
Ostatni przykład będzie dotyczył maszyny Truringa zwiększającej wartość liczby o 1. Poniżej zaprezentowano schemat takiego algorytmu:
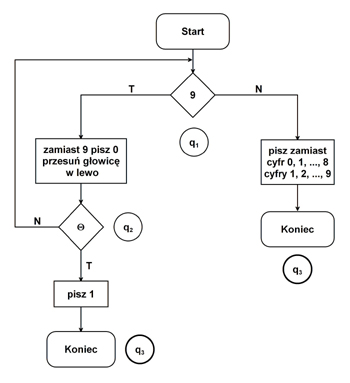
W komórkach poniższej tabeli zapisano instrukcje maszyny Turinga. Podobnie jak w pozostałych tabelach, kolumny zawierają dopuszczalne stany maszyny, zaś wiersze wszystkie symbole wejściowe.
Przedstawione powyżej proste przykłady ilustrują działanie maszyny Turinga. Istnieją też maszyny wielotaśmowe lub niedeterministyczne (gdzie jednej parze (stan, symbol) może odpowiadać wiele instrukcji.