Maszyna Turinga
Maszyna Turinga jest prostym matematycznym modelem komputera, służącym do wykonywania algorytmów. Został on wprowadzony przez Alana Turinga w 1936 roku.
Podstawowy model maszyny przedstawiony jest na poniższym rysunku:
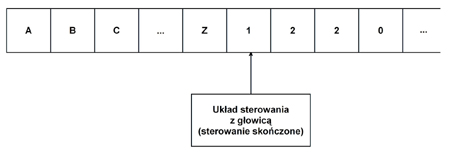
Posiada sterowanie skończone i składa się z taśmy wejściowej podzielonej na komórki, oraz głowicy, która może w danej znajdować się nad jedną komórką. Taśma ma komórkę położoną najbardziej na lewo, jednak prawostronnie jest nieskończona. Każda z komórek może zawierać dokładnie jeden symbol ze skończonej liczby symboli taśmowych. Pierwsze n komórek od lewej zawiera wejście, będące podzbiorem symboli taśmowych, zwanym zbiorem symboli wejściowych.
W zależności od symbolu, nad którym znalazła się głowica oraz stanu sterowania skończonego maszyna Turinga w pojedynczym ruchu:
zmienia stan
drukuje symbol w obserwowanej komórce taśmy, zastępując nim symbol uprzednio tam zapisany
przesuwa głowicę o jedną komórkę w lewo lub w prawo
Należy pokreślić, że maszyna Turinga, w przeciwieństwie do dwukierunkowego automatu skończonego, ma możliwość zapisywania symboli na taśmie.
Formalnie maszynę Turinga możemy zdefiniować jako:
M = ( Q, Σ, Γ, δ, q0, Θ, F )
gdzie:
Q - skończony zbiór stanów
Γ - skończony zbiór dopuszczalnych symboli taśmowych
Θ - symbol pusty należący do Γ
Σ - zbiór symboli wejściowych będący podzbiorem Γ niezawierającym
symbolu pustego B
δ - funkcja następnego ruchu będąca odwzorowaniem
Q × Γ w Q × Γ × { L, P } gdzie L i P oznaczają kierunek
ruchu głowicy w lewo lub prawo
q0 - stan początkowy należący do Q
F ⊆ Q - zbiór stanów końcowych
Maszyna Turinga jest uniwersalnym i powszechnie akceptowanym modelem formalnym efektywnej procedury. Nie można formalnie udowodnić, że jej model jest równoważny z naszym rozumieniem pojęcia komputera, jednak istnieje bardzo wiele argumentów przemawiających za tą tezą, nazywaną tezą Churcha. Należy zaznaczyć, że maszyna Turinga pod względem możliwości obliczeniowych jest równoważna ze znanymi dziś maszynami cyfrowymi, a także większością ogólnych modeli matematycznych obliczenia.